DECEMBER 2022 - THE STANDARD ERROR
One question is often asked when determining the scope of field or laboratory tests. How much tests should we perform to be sure of the parameter value? Often experience or unreferenced design codes are used to determine the number of tests. This leads to mistakes. The solution is a proper understanding of the influence of additional measurements. The standard error is a simple and efficient way to gain this understanding.
TOPIC OF TODAY - #1 STANDARD DEVIATION & VARIANCE
The most common action that is performed after receiving a measurement dataset is calculating the mean and standard deviation. Sometimes the variation (standard deviation divided by the mean) is provided too This provides an indication of the size of the variability. Unfortunately this only gives information on the variability properties of one specific dataset. Next to that it only provides accurate insight if the dataset alligns with a gaussian distribution. In order to improve our works we use the standard error to check the variability of the mean parameter estimate:
In short: just looking at the mean and standard deviation of a sample set can be usefull for engineering but does not help in determining the scope of a future measurement campaign. For example, it is impossible to judge if twice the amount of measurements would lead to the same engineering input. Also it is impossible if half of the measurements would lead to wrong engineering input. Two statistical concepts will be used to gain insight in the required amount of measurements: standard error and bootstrapping. Check out a previous blog for an explanation on bootstrap analyses if you are not familiar with the concept.
TOPIC OF TODAY - #2 STANDARD ERROR
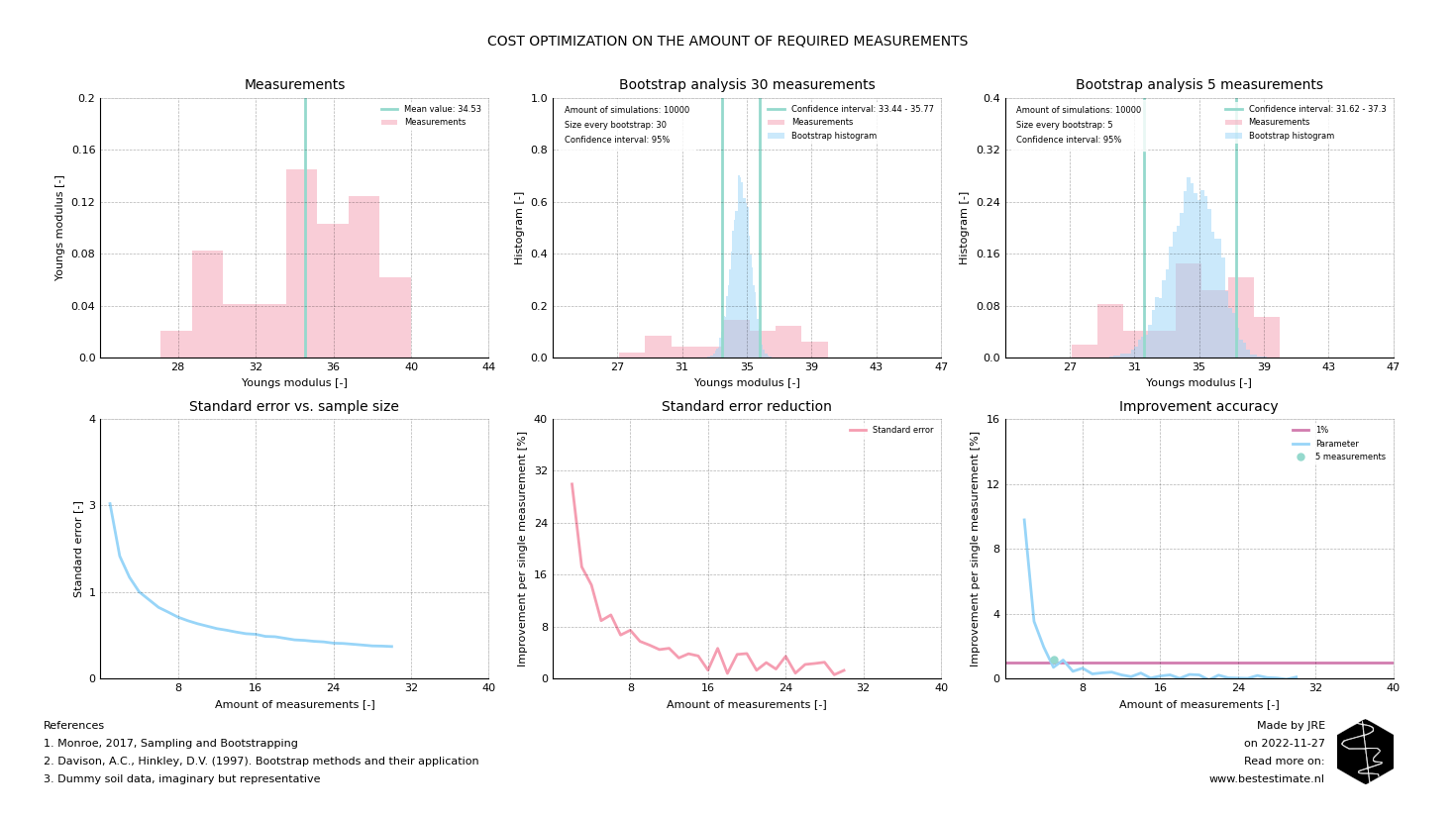
The standard error in combination with a bootstrap analysis provides an objective criterium to check if sufficent measurements are performed. This is especially relevant if measurements are costly or time intensive. This is often the case in our industry. As a case study we are looking at 30 existing measurements of the Youngs modulus, a stiffness parameter for soils. The procedure to set a scope for future measurements works like this:
- Take an original dataset and collect all measurements performed in similar conditions
- Determine which amount of accuracy gain you want to get from each additional measurement, for example 1%
- Perform a bootstrap analysis to obtain the accuracy of the mean of the total data set
- Perform the bootstrap analysis again with a the previous bootstrap size minus 1
- Repeat this step untill all analyses are completed, report the standard error per step
The result is a figure as presented below. As you can see the standard error reduces when the sample size increases. One can also see the error of the mean (standard error) already becomes more or less constant after 10 measurements. Most importantly the improvement of the mean parameter estimate is only <1% for each additional measurement after 5 completed measurements. This means that, provided that you are only interested in the mean value of a parameter, only several measurements are required.
FOOTNOTE
Please note that I run this service besides my job at TWD. It is my ambition to continuously improve this project and publish corresponding blogs on new innovations. In busy times this might be less, in quiet times this might be more. Any ideas? Let me know!
