SEPTEMBER 2022 - REGRESSION
Fitting a line to data is performed by engineers on a daily basis. In most cases, this is based on linear regression and the person fitting only needs to click a button. Howver, using regression requires much more nuances, especially when uncertainties and outliers play a role in your input data. This blog displays the application of several (robust) regression algorithms which are a better alternative in those cases.
TOPIC OF TODAY -#1 LINEAR REGRESSION
Linear regression is (without a too deep dive in the math) a way to fit a line through data while minimizing the overall absolute squared error. Note that this means that the goodness of fit of the line is determined based on sum of squared values of the errors. Since the algorithm is simple, it is integrated in many software applications. Linear regression can work perfectly, mainly when:
- There are no outliers in the measured data
- There is little variation in the data
- The variation that is present, is distributed evenly around the fitted line
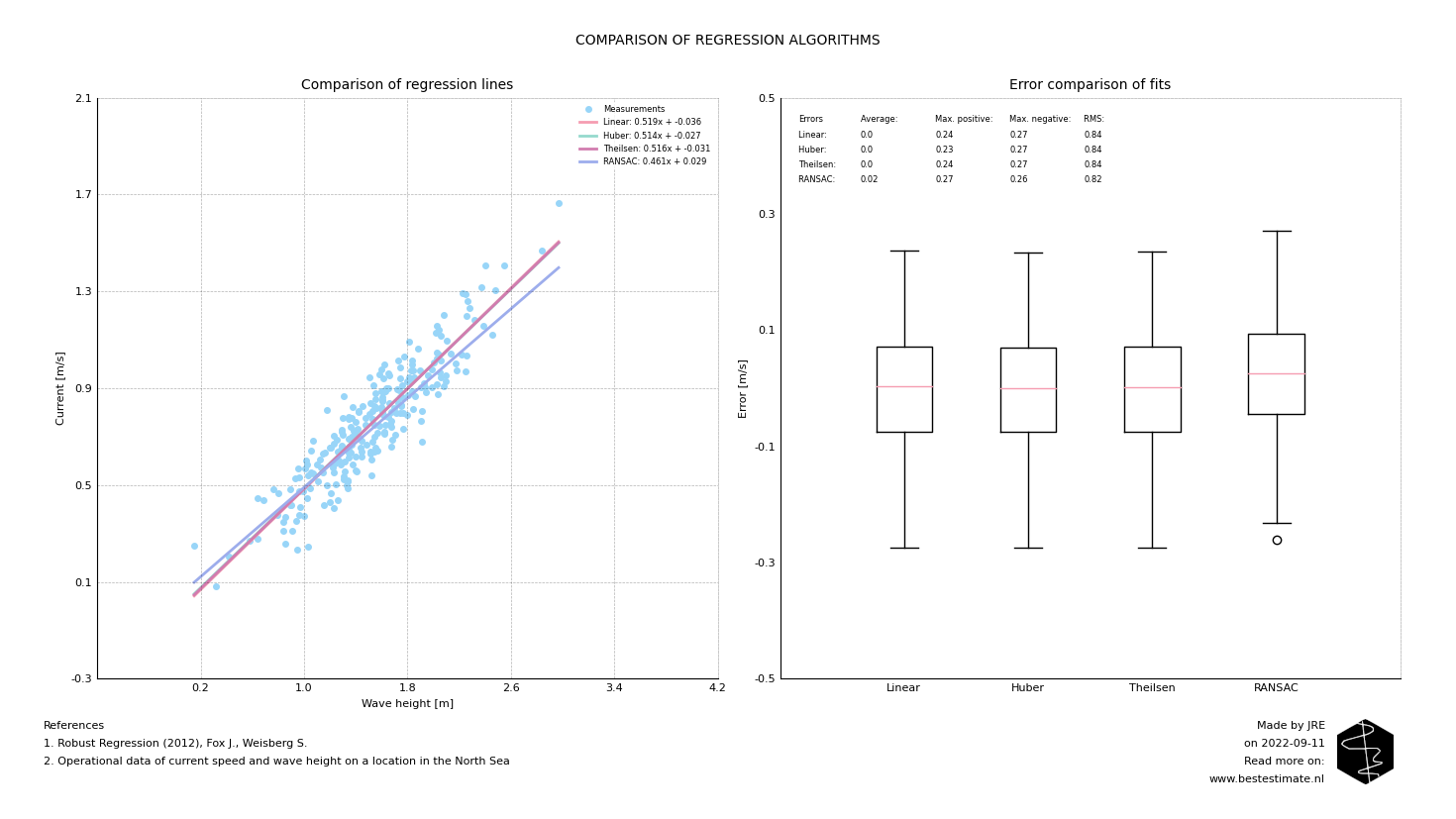
This is the case for the fitting exercise presented below. A linear function is fitted to the wave height and current measurements. In this case the error is pretty much normally distribued. As a consequence the fitted line with linear regression is good. Current can be reasonably predicted based on the wave height using the linear regression fit.
TOPIC OF TODAY -#2 ROBUST REGRESSION
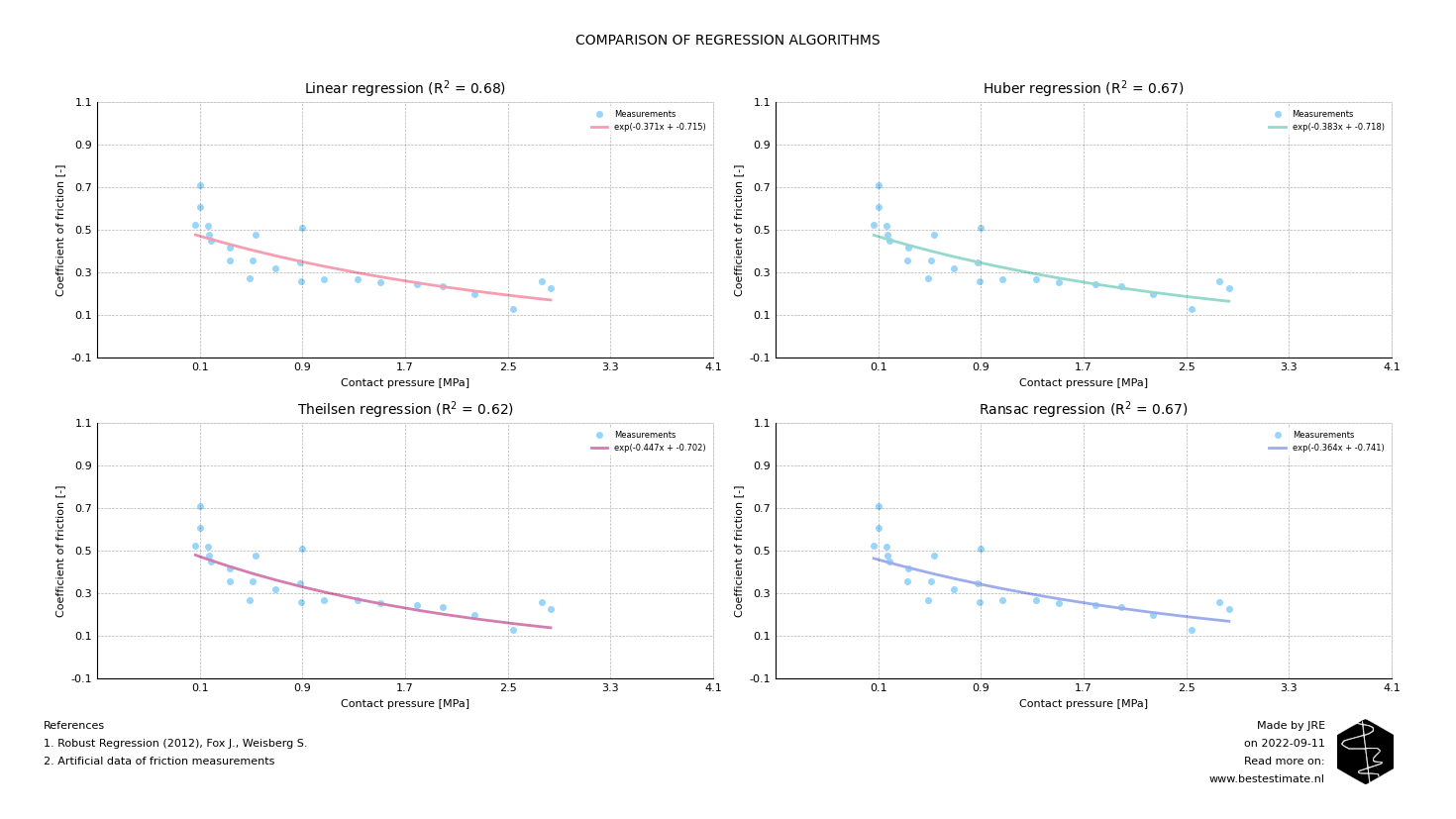
In many cases the conditions which are ideal for linear regression (like above) do not occur. This is especially the case for measurements on system characteristics like friction, wear and corrosion. In these cases there are many different things which can distort and create variability like: roughness, wetness, temperature, humidity. Linear regression is especially affected by outliers, due their quadratic contribution to the overall error. Therefore many alternatives (e.g. Huber, Theilsen, Ransac regression) have been invented to fit curves in a more robust manner. Below figures shows a couple of friction measurements and the fit proposed by these algorithms. Notice the differences?
The robust regression methods perform better as displayed in the error statistics below. Although their average error migh be a bit higher, the overall fit is better. Therefore they result in better predictors of, in this case, the friction coefficient by means of the contact pressure. Especially the Theilsen algorithm outperforms the others and also provides a conservative fit. Note that, in case you want to actually quantify a lower bound profile, it can be better to use other methods like quantile regression which is discussed in this blog.
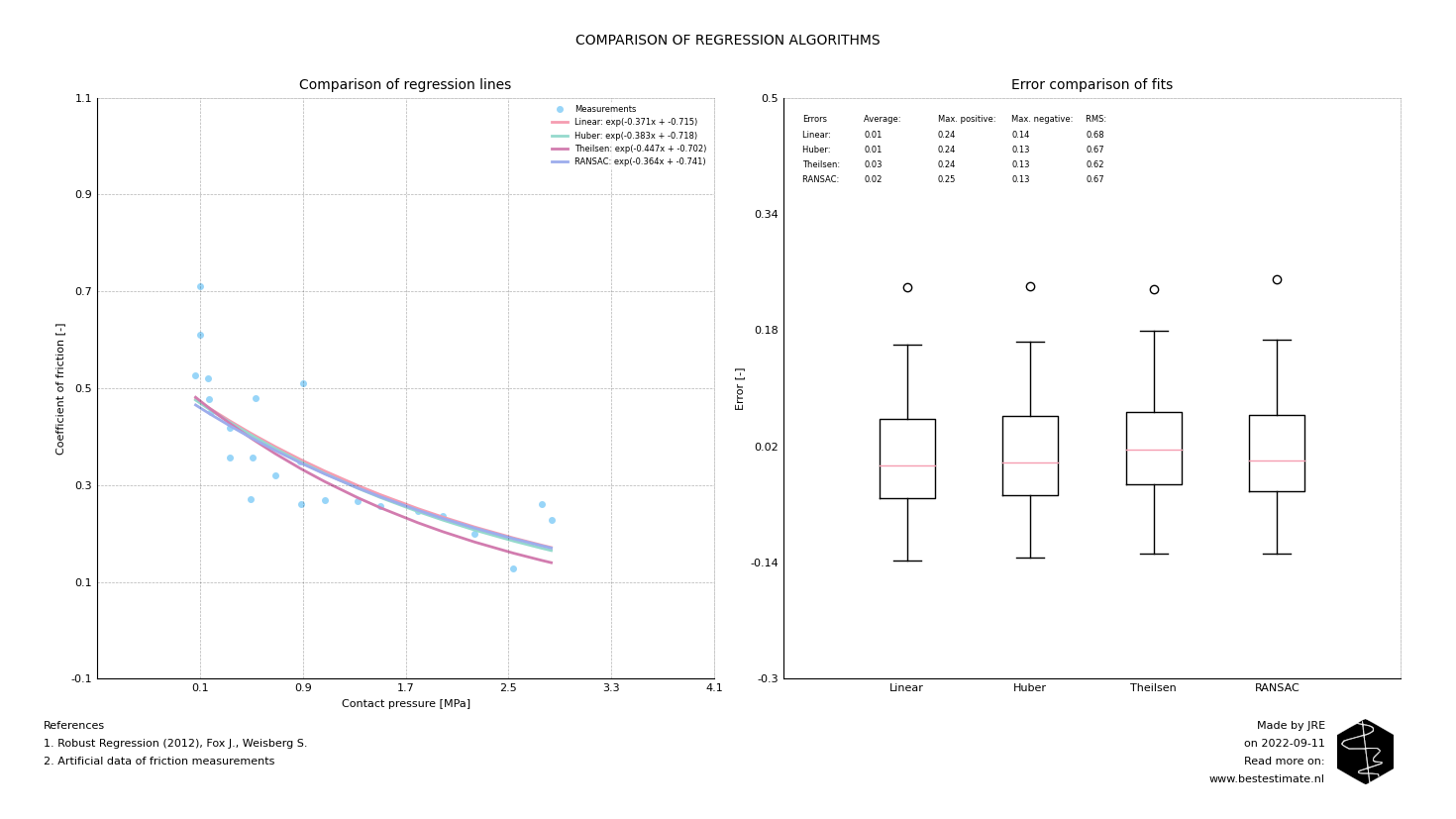
In these cases regression is applied to relatively simple two-dimensional problem, one input is used to estimate another variable. Note that regression is just as easily applied for predictors based on multiple variables. This is the reason that these kind of regression algorithms are used in a large amount of statistical applications.
FOOTNOTE
Please note that I run this service besides my job at TWD. It is my ambition to continuously improve this project and publish corresponding newsletters on new innovations. In busy times this might be less, in quiet times this might be more. Any ideas? Let me know!
