MAY 2023 - EXPECTED VALUES
One thing heard a lot in our industry is the quote: this is conservative! But how do you actually determine conservative input? This blog elaborates on a relatively simple classical concept in statistics which is often misunderstood: expected values.
TOPIC OF TODAY - EXPECTED VALUES
The expected value is used a lot in statistics but is often misunderstood in the construction industry. Two common misconceptions arise. Firstly, the expected value is not the average of the simulations. If we compare it to the distribution of people's weight, heavier individuals can deviate significantly from the average, while thinner ones cannot be equally much thinner. Secondly, it is also not the value with a probability of exceedance of 0.5. If that were the case, it would actually underestimate people's weight. Instead, it represents the weighted average or, in other words, the most likely parameter if we simulate an infinite number of random events. The figure below illustrates how the mean of the samples changes as we obtain more and more samples from the distribution discussed in the previous blog.
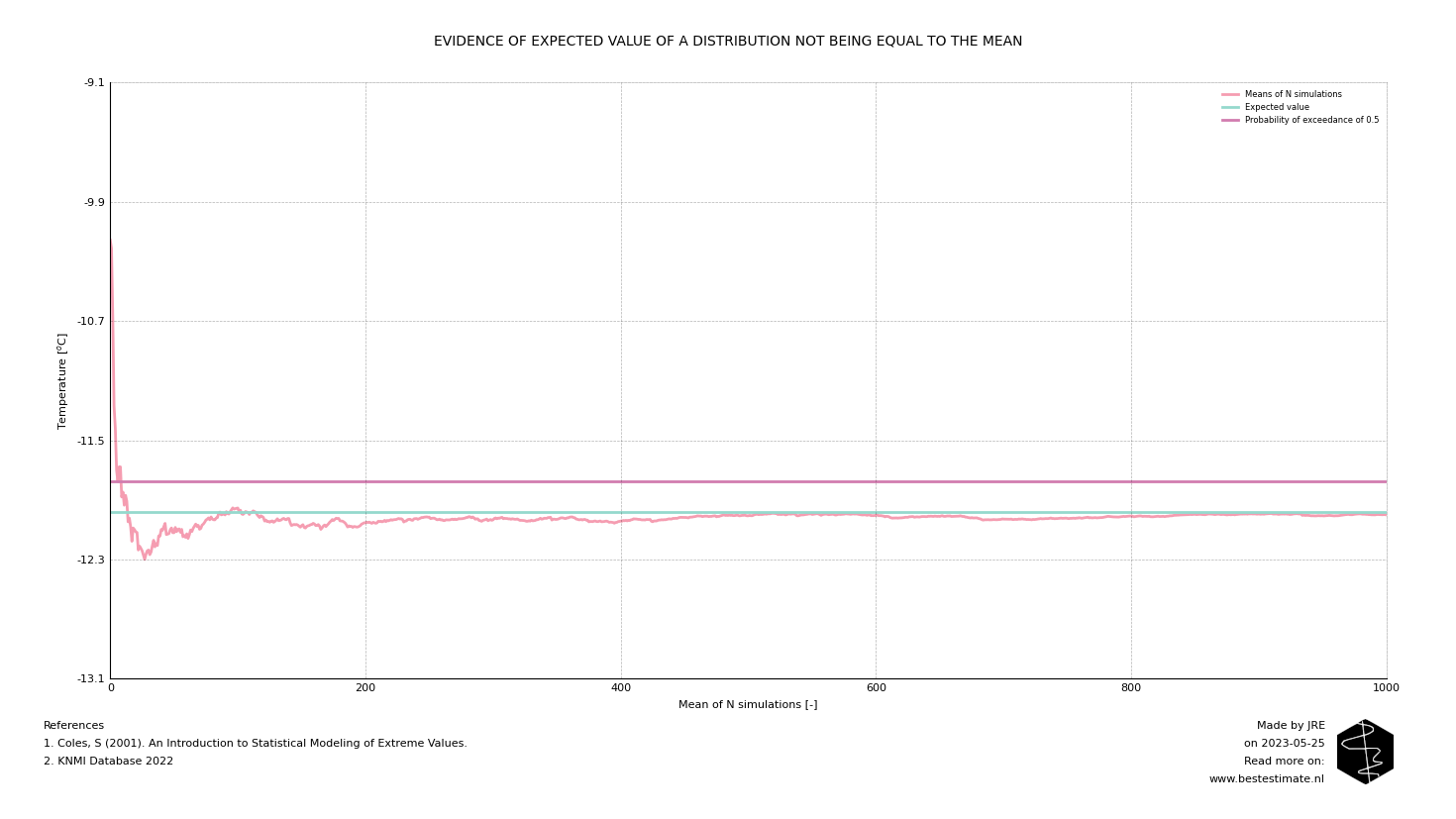
As you can see, the mean of the simulations approaches a constant value, which represents the expected value. The two wrong assumptions mentioned earlier only hold true for symmetric distributions, such as the normal and uniform distributions. However, when dealing with asymmetric distributions, things start to differ, as visible in the figure below. These distributions are known as asymmetric distributions. When estimating a value that is most likely to occur for a process, such as temperature or friction, it is advisable to use expected values, considering both extreme cases and average processes.

FOOTNOTE
Please note that I run this service besides my job at TWD. It is my ambition to continuously improve this project and publish corresponding blogs on new innovations. In busy times this might be less, in quiet times this might be more. Any ideas? Let me know!
