RELIABILITY ANALYSES & JOINT VARIABILITY
- How safe is my operation, what are the chances that something goes wrong?
- How can I most efficiently increase my workability?
- Which parameters influence my design or operation most and why?
- What should a safety factor for application be to allow for correct design?
Disclaimer. Privacy. Unsubscribe. Reach out.
Joint variability
Reliability analyses are often executed based on a concept called independence. In short this means that each variable is not related to another variable in your calculation. However, in reality variables can be very much related. One example is wind speed and wave height. Anyone who has ever been on a sailing boat knows that high wind speeds with low waves are unlikely. In soil mechanics engineering properties can also be correlated. These correlations should be properly quantified. Figure 1 shows a practical exaple for North Sea data.
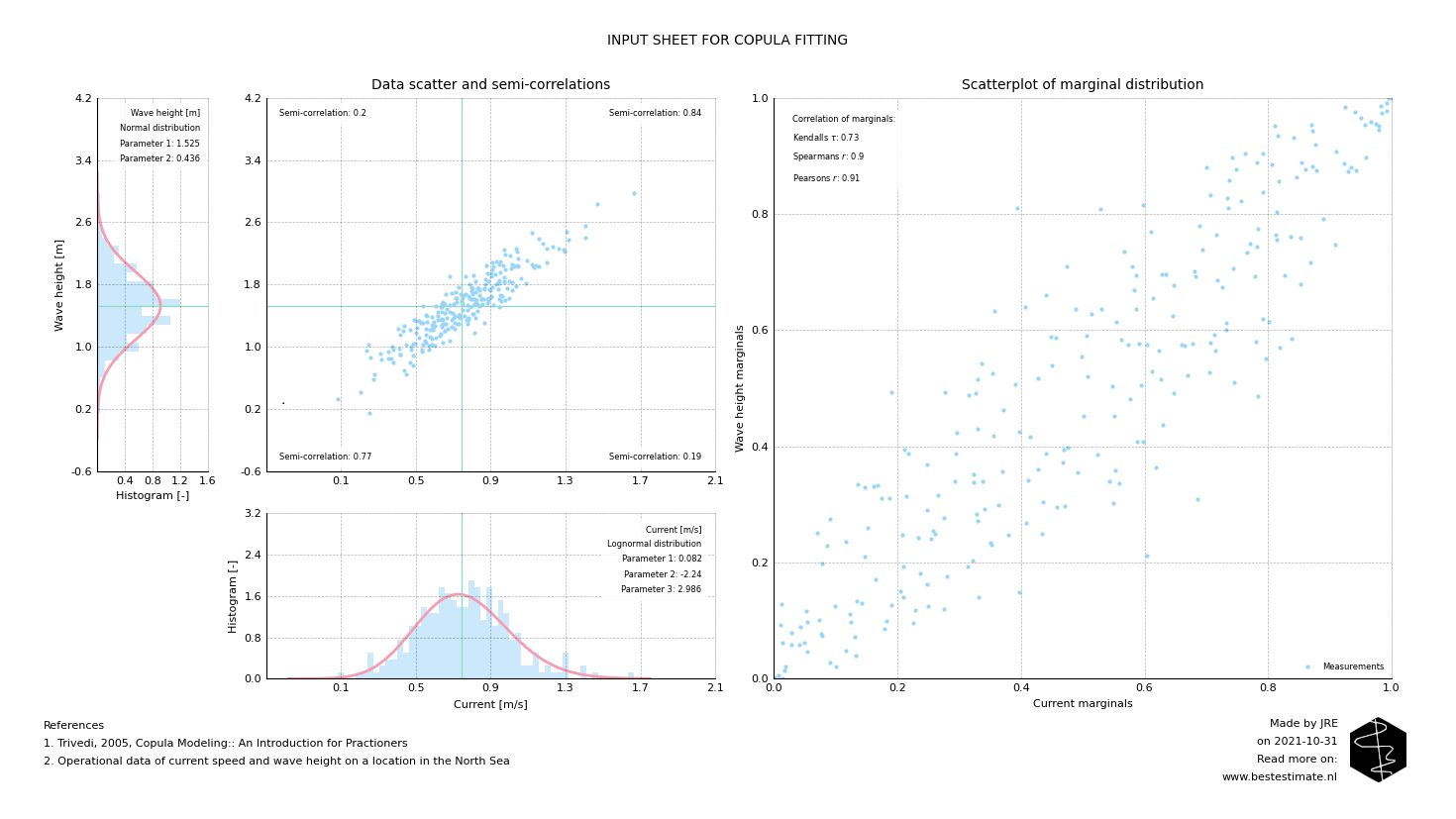
Figure 1, Obvious correlation between current and wave height at a North Sea measurement station
Figure 1 shows the correlation between current and wave loads. This correlation varies for the sizes of the waves and currents. These nuances can be quantified with Copulas. The API of Best Estimate incorporates four different types. In this case the Gumbel copula fits the data best. These correlations will be further used in reliability analysis. This is done to make sure that in case a high wave height is simulated, a high current is simulated too.
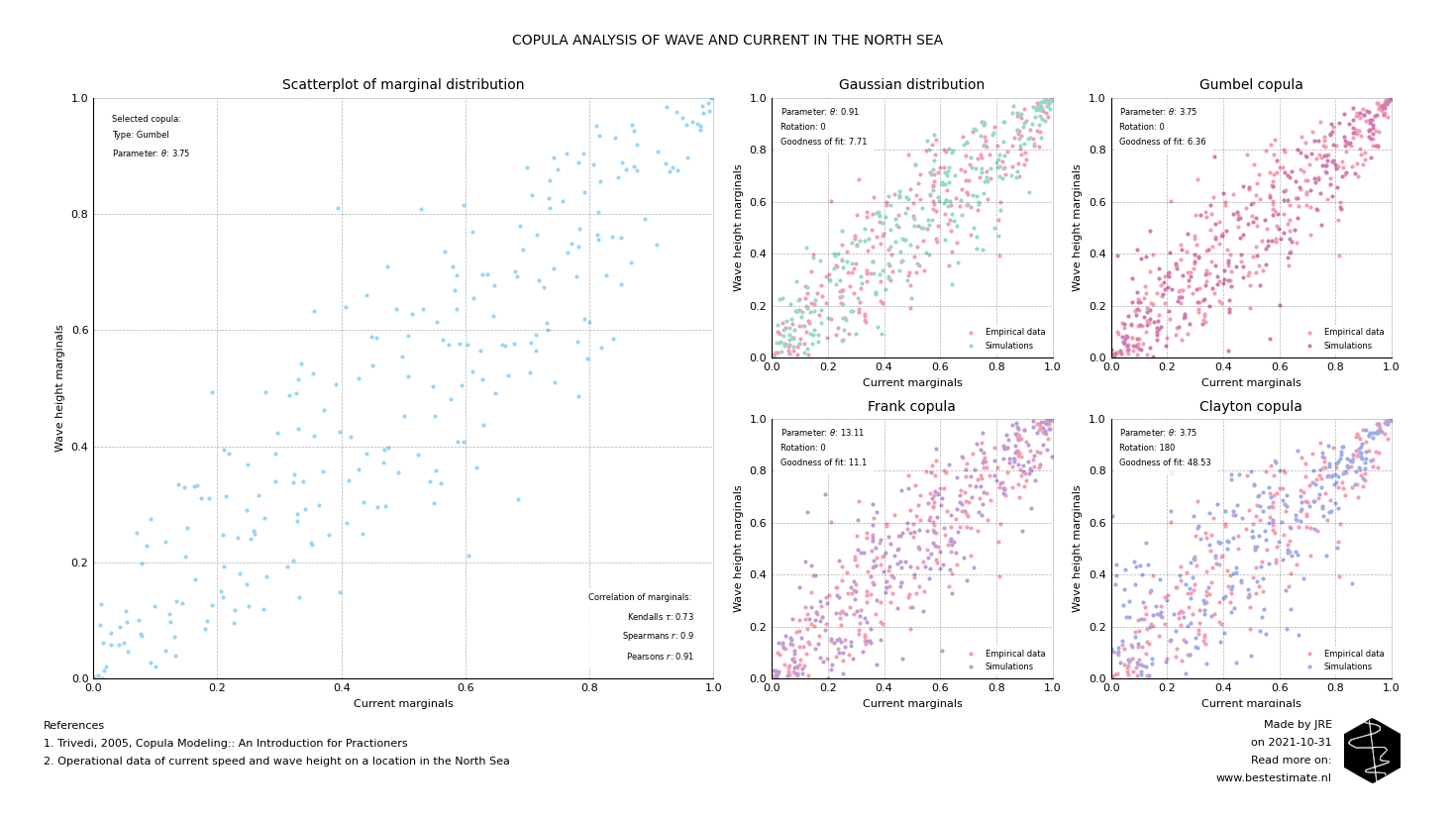
Figure 2, Comparison of fit of all Copulas. They can be rotated too if that fits the data better.
Monte carlo analysis including joint variability
The principle of a Monte Carlo analysis is well known. The probability of failure is calculated implementing the variability of all parameters and performing many different simulations. In the case of shallow foundation design, it would mean using probability density functions for the strenght and loading parameters. Not properly incorporating correlation structures can lead to unconservative or uneconomical design. This is why the Best Estimate API samples variables directly from the copula structures.
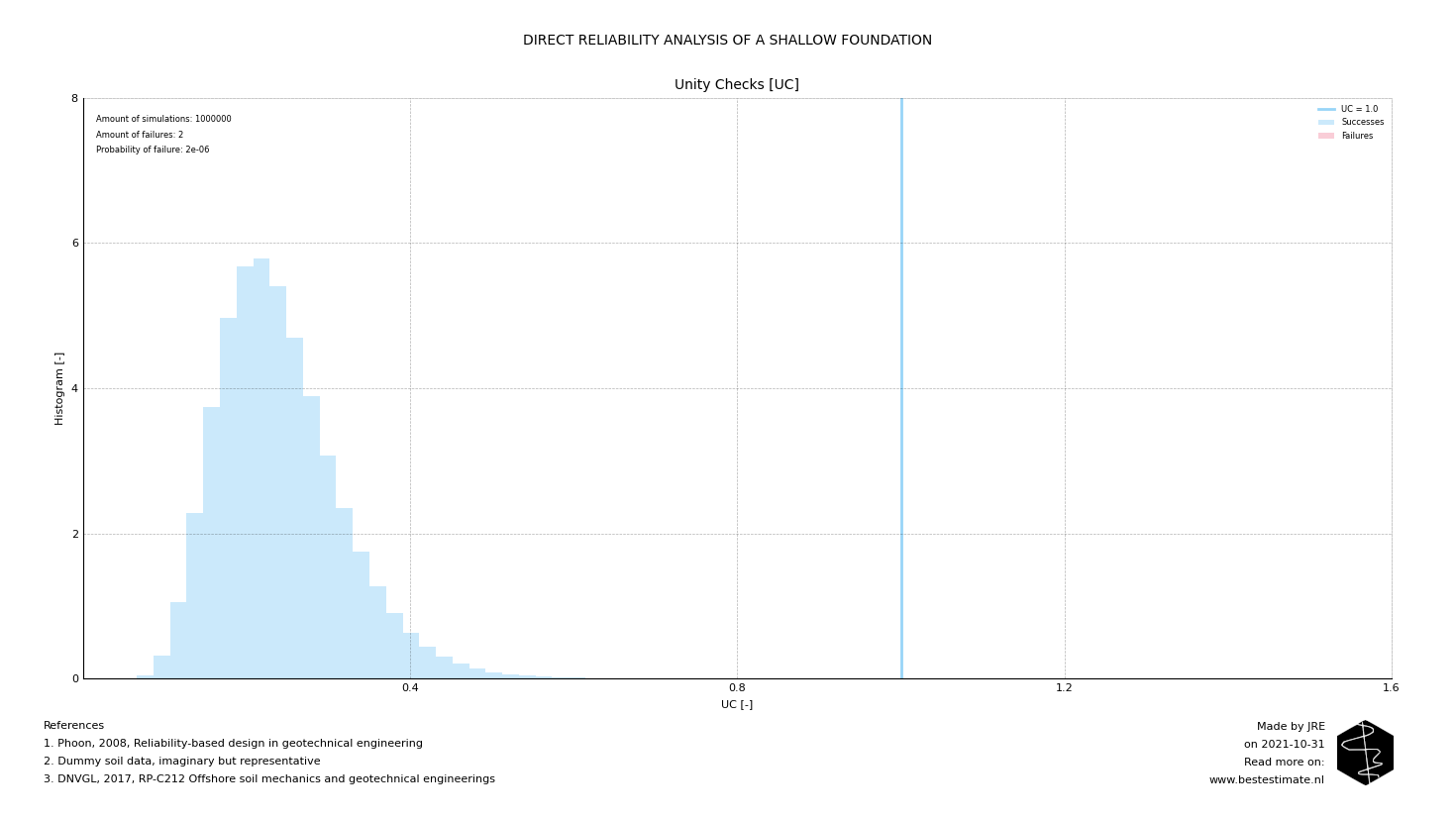
Figure 3, Results from a Monte Carlos simulations, 1 million Unity Checks plausible within variability of parameters
Table 1 shows the impact of the use of probabilistic methods compared to a deterministic design. A probabilistic approach leads to a reduced foundation surface area of almost 20%. This means that the foundation weight and consequential cost can also reduce with the same amount. The safety is still suffficient since it is realized while designing for a probability of failure of less than 1/10 million.
| Method | Required diameter | Required area |
|---|---|---|
| Conventional method | 7.2 m | 40.7 m2 |
| Probabilistic method | 6.5 m | 33.2 m2 |
Table 1, Impact of using probabilistic design methods on shallow foundation design
References
- DNVGL, 2017, RP-C212 Offshore soil mechanics and geotechnical engineering
- DNVGL, 2019, OS-C101 Design of offshore steel structures, general
- Phoon, 2008, Reliability-based design in geotechnical engineering
- Genest & Favre, 2007 Everything You Always Wanted to Know about Copulas
- Waterdata Rijkswaterstaat, 2021 (see this link)